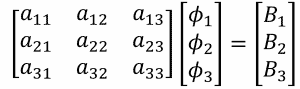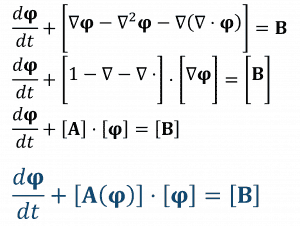Guts of CFD: CFD Linear Solution

The heart of any CFD program is an extremely efficient linear algebra solver. But CFD equations are non-linear. How do we stretch the limits of linear algebra to accommodate non-linear CFD equations? How do we take the mathematics from one cell and apply them to millions of cells?

Part 4:  CFD Linear Solution

1.0 Introduction

Computational Fluid Dynamics combines the elegance of mathematics with the raw processing power of the computer.  Previously, we covered the mathematics side:

1. Navier Stokes Equations
2. Interpolation Equations

But that elegance still lacks the power of the computer.  We need a way to apply the mathematics to millions and millions of equations, and then solve them efficiently.  Enter the CFD linear solver.

2.0 Linear Solution

Previously, we developed the mathematics for a single cell in computational fluid dynamics (CFD).  This mathematics created the differential equations for fluid flow.  We then added in the interpolation equations to convert calculus into algebra, so the computer understood it.  But this still required us to know the values in the surrounding cells.  Each cell in the simulation needs to know the value of its neighbors before we can solve it.  How to solve millions of equations, all coupled together?

With Linear Algebra.

2.1 Linear Algebra Solver

The heart of every CFD solver is a very efficient linear algebra solver, solving equations in the format of Figure 2‑1.  These programs need to be extremely efficient, since CFD simulations often solve matrices made from millions of equations.  One matrix for every transport equation in the simulation.  Take a moment to appreciate the massive magnitude of that matrix and the effort required to solve it.  That is why CFD developers invest heavily in shaving microseconds from the linear solver operations.

3.0 Solving Non-Linear Problems

We encounter a problem when applying linear algebra to CFD equations.  Linear algebra only works on linear equations.  No exponents, functions, or other funny business.  Each variable may be multiplied by a scaling factor (the A matrix) and that is it.  How do we stretch the limits of linear algebra to accommodate non-linear CFD equations?

Iteration.  Equation 1 shows an example of converting a non-linear transport equation into a format suitable for a linear CFD solver.  The feature is that the matrix no longer strictly holds constants.  It is also a function of the variables that we solve.  Strictly speaking, this is not linear algebra.  But done carefully, it works.  By factoring out part of the variables, the remaining terms are suitable for the linear solver.

The solution process is iterative.  The CFD engineer first creates an initial guess at the fluid flow.  The CFD solver generates the matrix from that first guess and solves for the fluid flow.  The solver next updates the matrix based on the newly calculated solution and resolves.  This iteration continues, comparing the difference between updated solutions.  The CFD engineer determines when to stop iterations.

4.0 Conclusion

The heart of any CFD program is an extremely efficient linear algebra solver.  But CFD equations are non-linear.  To get around that problem, we factor out part of the non-linear problem and solve it with linear algebra.  Using iteration, this process works accurately.  This little sleight of hand in the equations allowed us to apply the extreme efficiency of linear algebra to the complexity of CFD equations.

5.0 References