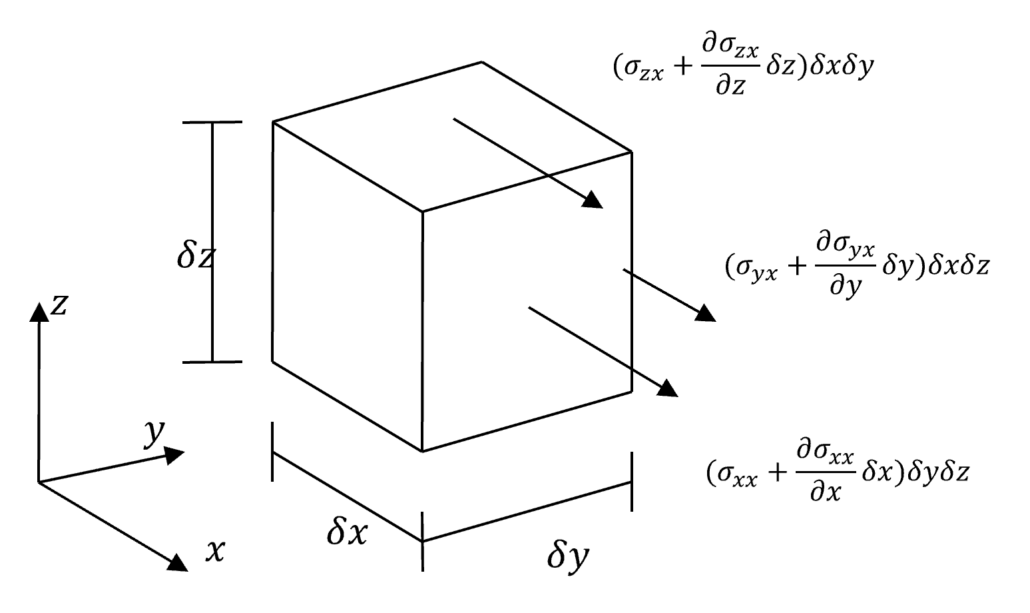
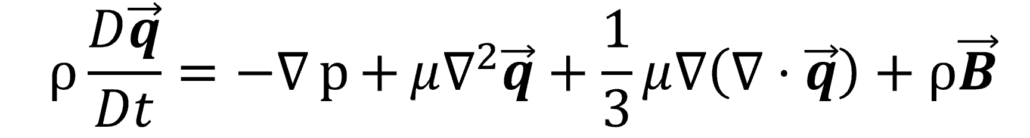Guts of CFD: Navier Stokes Equations

Navier Stokes Equation. Shrouded in mystery and intimidation. Navier Stokes is essential to CFD, and to all fluid mechanics. This equation defines the basic properties of fluid motion. But there is more to gain from understanding the meaning of the equation rather than memorizing its derivation. Today we review Navier Stokes Equation with a focus on the meaning behind the math.

1.0 Introduction

Navier Stokes Equation. Shrouded in mystery and intimidation. Speak their name and watch an engineer grimace with haunted memories of fluid dynamics classes. Navier Stokes is essential to CFD, and to all fluid mechanics. This equation defines the basic properties of fluid motion. But there is more to gain from understanding the meaning of the equation rather than memorizing its derivation. Today we review Navier Stokes Equation with a focus on the meaning behind the math.

2.0 Newton’s Law of Fluid Motion

The fundamental concept behind Navier Stokes equation is that it originated from Newton’s Law of Motion, but applied to a fluid.

To begin, start by adding all the forces that can apply to a small cube of fluid. We assume this is a very tiny cube of fluid. Eventually, the cube will become infinitely small as we involve calculus.

To keep the math simple, we will start by only considering forces in one direction, the X-direction. There are two types of forces to consider:

Surface forces
Body forces

2.1 Surface Forces

For surface forces in the X-direction, only six forces are possible. (Figure 2‑1) Because the cube is so small (soon to be infinitely small), no moments are possible, and no rotational motion develops.

Direct pressure on the X-face, positive side.
Direct pressure on the X-face, negative side.
Shear stress on the Y-face, positive side.
Shear stress on the Y-face, negative side.
Shear stress on the Z-face, positive side.
Shear stress on the Z-face, negative side.

After adding up all the surface forces, and simplifying the equation, you get a relatively simple expression for surface forces in the x-direction. (Equation 1)

2.2 Body Forces

Body forces act through the entire volume of the fluid cube. These include forces like gravity or magnetism. CFD engineers also use these to create artificial forces, referred to as source terms. The mathematical definition depends on the force term. For the basic definition of Navier Stokes, just remember that they exist as a placeholder. (Equation 2)

3.0 Navier Stokes – Derivation

The previous section identified all the forces acting on the fluid cube. But Newton’s law of motion equates force with mass and acceleration.

Mass is the fluid density times the dimensions of the fluid cube.

Acceleration gets defined in terms of calculus, by the total derivative.

Force is the summation of the surface forces (f1x) and the body forces (f2x).

Combine these three terms together and apply some algebra to simplify the equation. You get the equation for fluid motion in the X-direction. (Equation 3)

4.0 Full Definition for Fluid Flow

The full derivation for Navier Stokes equations requires several more steps. Plus, you need to consider the Y- and Z-directions. They follow the same process as the X-direction, with the variables adjusted. At this point, mathematicians normally shift to vector notation, which provides a condensed format to represent all three directions simultaneously. This article will not cover the full derivation, because the meaning behind the math is more important in this case. Equation 4 shows the full equation for Navier Stokes. That equation looks complicated, but the core principle remains mass times acceleration equals force.

All the terms on the right-hand side represent forces. Density (ρ) on the left-hand side represents mass. And the total derivative on the left-hand side represents acceleration.

4.1 Full Definition of Fluid Domain

The Navier Stokes equation was a major victory for mathematics of fluid mechanics. That defined the fundamental mathematics for fluid motion. Couple this with three other sets of equations and get the four sets of information required to completely define everything about a fluid flow in a domain:

Navier Stokes Equation
Equation of Continuity
Any thermodynamic relationships
Boundary conditions

In practical terms, the equation of continuity specifies that fluid cannot simply disappear or pop into existence. It can change in density, expand and contract, but there are no wormholes in conventional fluid flow.

The thermodynamic relationships address those changes in density, reactions to heat, temperature, etc. They also include buoyancy effects.

And the boundary conditions specify the limits of our domain. They help us solve the differential equations. In practical terms: Imagine a glass fruit bowl filled with deep blue water. The glass containing the water is a boundary condition. That containment gets expressed as a math equation.

Solve these four sets of equations, and you know everything about that fluid flow, which is an incredibly impressive achievement.

5.0 Conclusion

At its core, Navier Stokes equation is simply Newton’s Law of Motion, applied to fluids. The math gets complicated, but the principle remains the same.

6.0 References

[1]	V. R. Raj, “Quadratic Profile Used in QUICK Scheme,” Wikimedia Commons, 12 Nov 2012. . Available: https://commons.wikimedia.org/wiki/File:Quadratic_profile.jpg. .
[2]	Max Pixel, “Cumulus Storm Turbulence Thunderstorm Cloud Roller,” Max Pixel, 01 Jan 2019. . Available: https://www.maxpixel.net/Cumulus-Storm-Turbulence-Thunderstorm-Cloud-Roller-567678. .
[3]	S. Wasserman, “Choosing the Right Turbulence Model for Your CFD Simulation,” Engineering.com, 22 Nov 2016. . Available: https://www.engineering.com/DesignSoftware/DesignSoftwareArticles/ArticleID/13743/Choosing-the-Right-Turbulence-Model-for-Your-CFD-Simulation.aspx. .
[4]	Q. Wang, C. Yan and T. Hui, “Mechanism Design for Aircraft Morphing Wing,” Research Gate, , Accessed: 2019, Jan, 01, April 2012.
[5]	S. Tao, F. Yuqing, L. Graeme and J. Kaixi, “CFD simulation of bubble recirculation regimes in an internal loop airlift reactor,” in 27th International Mineral Processing Congress, , Accessed: 2019, Jan, 01., January 2014.

Guts of CFD: Navier Stokes Equations

1.0 Introduction

2.0 Newton’s Law of Fluid Motion

2.1 Surface Forces

2.2 Body Forces

3.0 Navier Stokes – Derivation

4.0 Full Definition for Fluid Flow

4.1 Full Definition of Fluid Domain

5.0 Conclusion

6.0 References

Share This Post

More Like This

Surviving the Arctic: Polar Class Icebreakers

Ramming the Ice: Icebreaker Propulsion

Ever Given: What We Don’t Know

Stability Letters Explained

Free Surface Moment

Practical Stability Test: Naval Architect’s Guide

Stability Test Theory

Practical Stability Test: Chief Engineer’s Guide

Practical Stability Test: Master’s Guide

Our Socials

About Us

What We Do

Contact Us