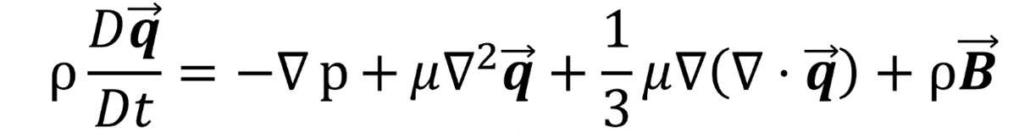Guts of CFD: Transport Equation

What is the utility of a transport equation? What do they achieve? Transport equations form the fundamental language of computational fluid dynamics (CFD). CFD engineers use them to communicate ideas, program CFD software, and diagnose problems with their simulations. But they only work if you understand the language. Today we...

Part 2:  Transport Equations

1.0 Introduction

What is the utility of a transport equation?  What do they achieve?  Transport equations form the fundamental language of computational fluid dynamics (CFD).  CFD engineers use them to communicate ideas, program CFD software, and diagnose problems with their simulations.  But they only work if you understand the language.  Today we explain transport equations and the significance of their terms.

2.0 Navier Stokes to Transport Equation

A transport equation is any differential equation for any variable that we solve in CFD.  But don’t assume one interpretation of the phrase.  The term “transport equation” conjures several different levels of expression in CFD.

1. Two engineers are communicating.  They use a “transport equation” as loose math, emphasizing the derivatives of an equation and ignoring the other terms.  Engineers may do this to help communicate a concept.
2. A more rigorous definition.  The exact and precise transport equation, represented in vector notation, with all terms defined.  Mathematically accurate, but too abstract to encode into CFD software.
3. A programmatic definition.  The transport equation is defined for a single set of coordinates or matrix entry.  All terms are defined.  This is ready to encode into CFD software.  But it probably requires other equations for a complete definition.

We will use the Navier Stokes Equation as a starting template and convert that into a generalized transport equation. (Equation 1)  In this example, “transport equation” means the first definition, loose math that emphasizes the derivatives and ignores the other terms.  The end goal is to regroup the equation and highlight different classes of derivatives.

To convert the Navier Stokes equation in to a generalized transport equation, we do several things.

1. Drop the pressure term.  The main variable transported in this equation is velocity.  We want to emphasize the relationships with velocity.  And the pressure gradient is special to Navier Stokes.  (Remember, loose math.)   
2. Swap out the letter q (velocity) for the letter phi φ. Phi is the general symbol used in transport equations.  It stands as the universal signal that this is a generalized transport equation.  You will know the definition of phi by knowing what each transport equation addresses.
3. Take the total derivative and break out time from the rest of the spacial derivatives.
4. Drop any constant terms (1/3μ).  Not relevant to our purpose of emphasizing the derivatives.

After those steps and some rearranging, we arrive at the transport equation for velocity. (Equation 2)

Is this the correct transport equation for Navier Stokes? NO!  We used loose math to create a generalized transport equation based on Navier Stokes.  The purpose was to communicate a concept.  The terms of that transport equation are grouped into four distinct and important groups.

3.0 Transport Terms

The four terms in the transport equation behave in very different ways. (Figure 3‑1)  When these equations get encoded into CFD software, it becomes very important.  The different differential terms (gradient, Laplacian, curl) each have different algorithms inside the CFD software.  As the CFD engineer, you need the ability read a transport equation, identify these categories of terms, and understand how they apply to the weaknesses of your CFD software.  The following sections explain each category.

3.1 Time Variation

The time variation term determines how the variable changes in time.  If this term dominates your transport equation, pay attention to how the solver handles the time interpolation.  Options include explicit or implicit time integration.  Implicit time integration allows larger timesteps.  Explicit time integration is necessary for very fast events that happen in milliseconds.  Little more needs to be said at this introductory level.

3.2 Convective Terms

The convective terms are the derivatives that maintain a continuous line of transport.  Imagine a set of billiards balls.  The convective terms would be responsible for the billiards balls each colliding in a straight line.  Alternatively, the diffusive terms handle the collisions to the side that spread outwards. 

Convective terms include the major streamline flow patterns.  They follow the flow along the streamline.  Interpolation equations for convective terms normally work better at higher Reynolds numbers (1×10⁴ and higher).  If you see problems with following simple streamlines, and your simulation works at low Reynolds numbers, check to see if convective terms are a major feature in your transport equation.

3.3 Diffusive Terms

The diffusive terms handle diffusion to the side.  This includes viscosity effects, turbulence, and particle rotation.  The interpolation equations for diffusion typically tune to work better at lower Reynolds numbers.

3.4 Source Terms

The source terms create (or destroy) your transport quantity.  This is not the same as creating matter.  In the case of the velocity transport equation, the source term generates new momentum, effectively increasing velocity without increasing mass.  Source terms are an infrequent item, used only for special cases.  Often the CFD engineer intentionally specifies a source term as a simple approximation for more complicated physics.

4.0 Conclusion

Transport equations are not a technique or specific equation to memorize.  They are the alphabet.  They appear as a common language of communication in CFD.  CFD engineers use them to emphasize concepts, as done in this article, or to document specific equations for programming into software, and many more applications.  As the CFD engineer, you need to read a transport equation, identify the different derivatives, and recognize how those derivatives may impact your specific simulation.  The world of CFD has vast references and helpful articles waiting to assist you, but only if you can read the language.

5.0 References