Hydrodynamics and Hull Design

A refined hull shape epitomizes the link between tradition and science. When we link the science of ship design with the experience of past ships, we identify the successes and isolate previous failures. This article glimpses into the background of hydrodynamics by exploring the link between the science of Bernoulli’s equation and the shape of...

Linking Hull Shape to Powering

Ship science links the heritage of maritime design, and the potential of modern scientific knowledge.  A refined hull shape epitomizes that link between tradition and science.  A modern naval architect carefully designs the hull shape based on previous examples and the science of hydrodynamics.  This article glimpses into the background of hydrodynamics by exploring the link between the science of Bernoulli’s equation and the shape of ship hulls.

1.0 Bernoulli’s Equation

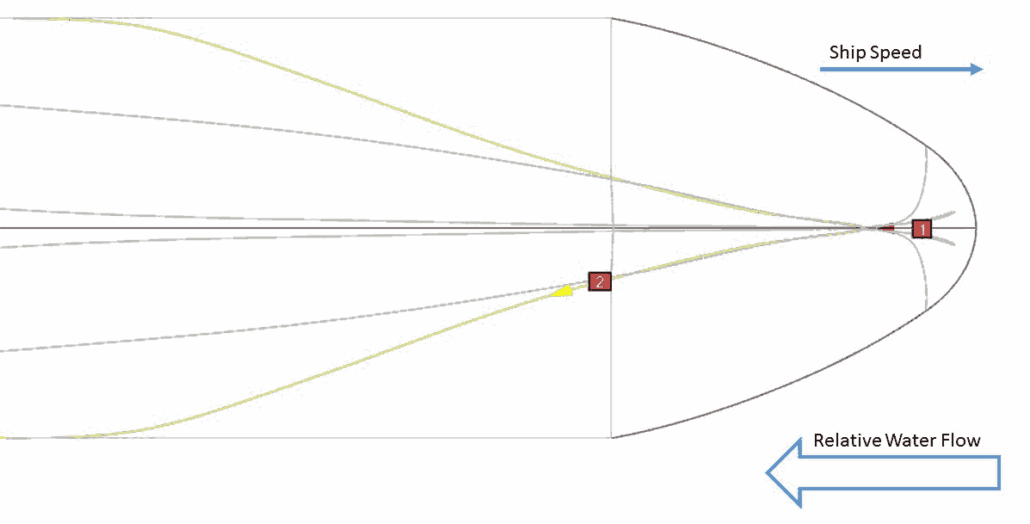
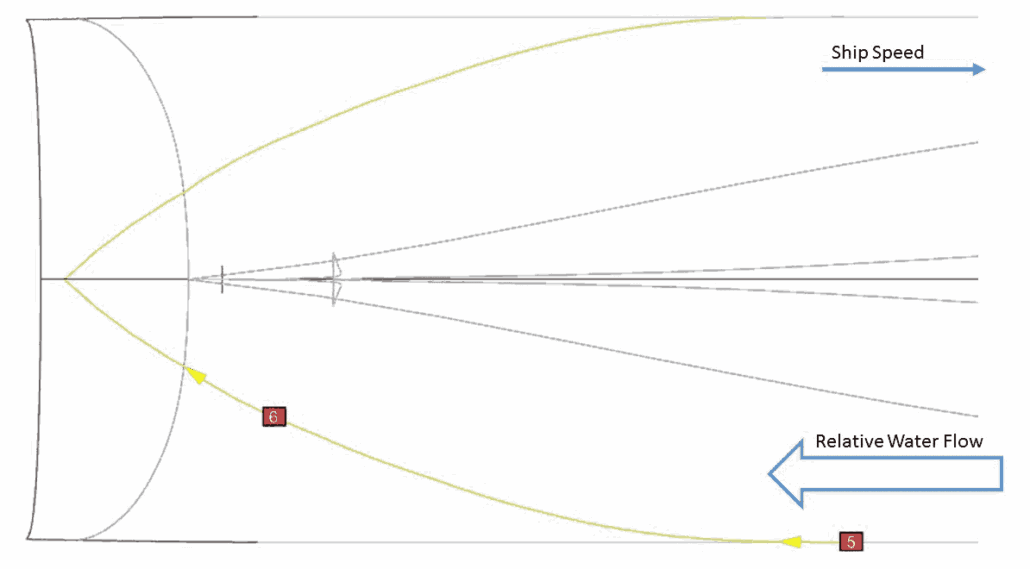
The basis for all fluid mechanics is Bernoulli’s equation. (Equation 1 [1])  It describes the various forms of energy that a fluid can hold, making it synonymous to enthalpy equations in thermodynamics.  Except Bernoulli’s equation factors out all the constant terms and we discover that energy in a fluid measures as a pressure, in various forms.

Where:
p =                          Pressure, from compression of fluid (Pa)
ρ =                          Density of fluid (kg/m³)
g =                          Acceleration due to gravity (-9.8065 m/s²)
z =                          Vertical distance above reference point (m)
q =                          Fluid velocity, combination of all three directions (m/s)

This equation shows that a fluid holds pressure in three possible forms:  compression of the fluid, hydrostatic pressure, or velocity of the fluid.  (This is a simplified version of the equation meant for steady flow.  Other terms add in if we consider unsteady flow.)  All three pressure terms add up to a constant, which means that pressure along a streamline can change forms, but it always adds up to the same total.  (The only exception is when we intentionally add energy to a fluid with a pump or other device.)  Bernoulli’s equation is more accessible when we recognize it as the sum of three categories of pressure (Equation 2):

Compression + Hydrostatic + Velocity = Constant (Equation 2)

We use Bernoulli’s equation most often to compare changes at different points along a fluid streamline.  When comparing two points, the total is not important.  We focus on how the fluid pressure shifts between categories when transitioning between the two points.  (Equation 3)

Compression1 + Hydrostatic1 + Velocity1 = Constant = Compression2 + Hydrostatic2 + Velocity2 (Equation 3)

For hull design, the most important term is the pressure from compression of the fluid.  That compression pressure is what pushes on our hull.  The drag of ship resistance begins here.  We need one more element to convert compression pressure into resistance.

1.1 Direction Matters

The pressure from compressed fluids acts as a pressure on the hull.  But not all of that pressure shows up as resistance.  Pressure pushes equally in all directions; the orientation of the hull surface determines the direction of that force.  Figure 1‑1 shows a typical pressure variation around a propeller blade.  The magnitude of those arrows shows the changing pressure, which is governed by Bernoulli’s equation.  Notice how the direction of the arrows follows the orientation of the surface.

2.0 Flow at the Bow

The trick for hull design is to minimize the changes in water velocity.  We want nice smooth changes.  Of course, some velocity change remains inevitable.  Our second strategy is to ensure the hull surface orients so that any changes in pressure do not push longitudinally.  Any longitudinal forces add up to increase the ship resistance.

Trace the path of flow along the yellow waterline in Figure 2‑1.  Compare the flow directions at points 1 and 2.  Point 1 flows purely longitudinal.  But point 2 shows the flow vectoring off transverse.  Moving from point 1 to 2, the following changes happened.

1. Reduced velocity pressure from longitudinal direction
2. Increased velocity pressure from transverse direction
3. Increased compression pressure on hull surface
   1. Hull surface oriented at approximately 15 deg to longitudinal
   2. Only 26% of pressure acted longitudinally, adding to resistance

Some of the reduction in longitudinal velocity transferred over to transverse velocity, but not all of it.  As this streamline tried to move transversely, it ran into the surrounding water.  Like lanes of traffic merging on the freeway, both fluid streams slowed down before the merge.  The remaining pressure transferred into compression pressure, which added to the ship resistance.

This example did require oversimplification, but it still illustrates how Bernoulli’s equation depicts pressure changes due to hull shape.  The actual flow patterns require us to consider several other elements:

1. Vertical flow velocity
2. Changing hydrostatic pressure due to ship waves
3. Pressure field altering flow patterns upstream

In reality, several other physics interact to produce the final flow patterns.  DMS utilizes advanced tools like computational fluid dynamics (CFD) to accurately predict these interactions and resulting complex flow patterns.  But we still use Bernoulli’s equation to convert those flow patterns to changes in fluid pressure.

3.0 Flow at Midships

Figure 3‑1 shows typical flow lines along the midship of the hull.  Moving from point 3 to 4, nothing appears to change.  The flow lines are parallel, which is why we call this the parallel midbody.  This section comes almost free of charge.  The parallel lines create no pressure changes and they have no longitudinal orientation that can add to resistance.

The parallel midbody does experience some losses due to skin friction, but this article just focused on pressure changes from shape of the hull.  The hull optimization process tries to maximize the length of the parallel midbody, without negatively impacting the bow and stern.  More parallel midbody means more hull for almost free.

4.0 Flow at the Stern

Some disregard flow at the stern of the vessel, which is an overlooked opportunity.  Start at point 5 in Figure 4‑1.  Flow from the parallel midbody returned to nearly the same as point 1 on the bow, free of any ship interference.  The majority of the pressure returned to velocity pressure.  Travelling downstream to point 6, several positive changes happen.

1. Reduced velocity pressure in the longitudinal direction
2. Mild increase in velocity pressure in the transverse direction
3. Large increase in compression pressure on hull surface
   1. Hull surface oriented at approximately 27 deg to longitudinal
   2. 46% of pressure acted longitudinally, reducing the total resistance

The increased pressure from compression pushes against the stern of the hull.  By pushing from the aft side, the pressure reduces the total hull resistance.  It pushes the hull forward.  We call this pressure recovery, and it is a vital component of efficient hull design.  The stern of the vessel can be more important than the bow.  Hull shape at the stern must be smooth with large radius bilges to allow gentle flowlines without generating excessive turbulence or recirculating flow patterns.  (This only applies to displacement hulls.  Semi-displacement and planing hulls operate under different physics.)  DMS devotes important time toward the stern shape to achieve suitable pressure recovery.

5.0 Conclusion

Designing the hull shape does not require magic; it uses science.  DMS utilizes Bernoulli’s equation and other hydrodynamic techniques to make informed decisions about the hull shape.  When we link the science of ship design with the experience of past ships, we identify the successes and isolate previous failures.  The link between science and ship design ensures confidence that each design improves beyond previous achievements.

6.0 References